符号执行和混合符号执行，以及一个混合符号执行引擎的实现

Posted on Oct 19, 2022

上个星期我看了一下 EXE 的论文，做了一下 cs6.858 的 lab3。大一的时候其实我就接触过符号执行，但是一直很遗憾没有自己实现过。所以又花了一个周末的时间写了一个混合符号执行的 demo。总的来说我觉得非常有意思。

Symbolic Execution

说到混合符号执行，不得不提的是符号执行。符号执行的思想很简单，计算机程序的分支结构都是二元的，循环和 switch 这样的结构，最后也会转换成二元分支。在二元分支上，选择路径时，都会根据特定的约束条件判断应该执行哪个分支，如果我们能够求出输入在什么取值下可以使约束条件成立，在什么取值下可以使约束条件不成立，就可以带着这样的取值条件分别进入两个分支，进而在碰到所有的分支都可以获得进入这个分支时的输入取值范围和路上被赋值的变量的取值范围。这样我们可以做到：

求出几组输入，这些输入可以让程序执行完所有可执行的路径，让我们获得很高的测试的覆盖率
求出每个变量在特定位置的取值范围，这样在变量用于危险操作，如做数组下标的时候，就可以判断可不可能出现越界访问

先以一个比较 trivial 的例子来看符号执行，假设我们需要测试的目标代码是这样一个函数

void test(unsigned int i) {
	unsigned t, a[4] = { 1, 3, 5, 2 };
	if (i >= 4)
		exit(0);
	char *p = (char *)a + i * 4;
	*p = *p − 1;
	t = a[*p];
	t = t / a[i];
	if (t == 2)
		assert(i == 1);
	else
		assert(i == 3);
	}

这个函数的输入就只是他的所有参数，也就是 unsigned int i，我们先把这些参数“符号化”，符号化比较类似于设未知数，我们设 i 的值为 $x$（实际上，一般我们会把变量的名字当作符号的名字，但是这里为了区分变量名和符号名，特意给两者取不同的名字）。

然后开始执行，首先我们会碰到第一个分支，i >= 4，此时我们添加一个约束条件给 true branch，也就是 $x \geq 4$，然后 fork 执行流，进入 true branch，发现碰到了 exit(0) 正常退出，退出后调用求解器，求出当前约束条件下 i 的取值为 i >= 4，这样我们就探索出了一个路径。

接着，尝试进入 false branch，添加约束条件 $x < 4$，此时我们将计算出 p 的取值为 $ \&a + x * 4$ ，可见他是一个带符号的表达式。接下来会执行 *p - 1 的操作，在碰到指针操作的时候需要引入对内存的抽象，有许多对内存的抽象方法，EXE 是将内存看作没有类型的连续字节序列。不管怎么抽象，只要能够在这种情况下获得正确的约束条件就可以了。

由于 p 是指向 a 数组的指针，所以在对 p 解引用和对 *p 赋值的时候都需要添加在范围内和数组溢出的约束条件，我们称在数组范围内的约束条件为 in bounds(a[*p])，越界的约束条件为 out of bounds(a[*p])，这两个函数会帮我们添加正确的约束条件。这里我们不妨想一想应该添加怎么样的约束，如果不能越界，那么就是偏移不能超出数组的大小，也就是 $p - \& a < sizeof (a) \rightarrow x * 4 < 4 * sizeof(int)$ ，最后就会求解出 $x < 4$，同时下标不能为负，所以还要添加 $x \geq 0$ 的约束（当然实际上由于 $x$ 应该是无符号的 32bit 数，所以这个约束不会真正生效）。再结合之前的进入 false branch 的 $x < 4$ 的约束就可以求解出 $x$ 的取值为 ${0, 1, 2, 3}$ 时不会越界，可以继续执行。那么 out of bounds 就是反一下 in bounds 的约束了，这样可以求解出 $x = 4$ 时会出现数组越界。

继续往下执行，可以一步步分析出 i 在取什么范围的值可以执行到什么地方，也可以判断会不会有危险操作出现。

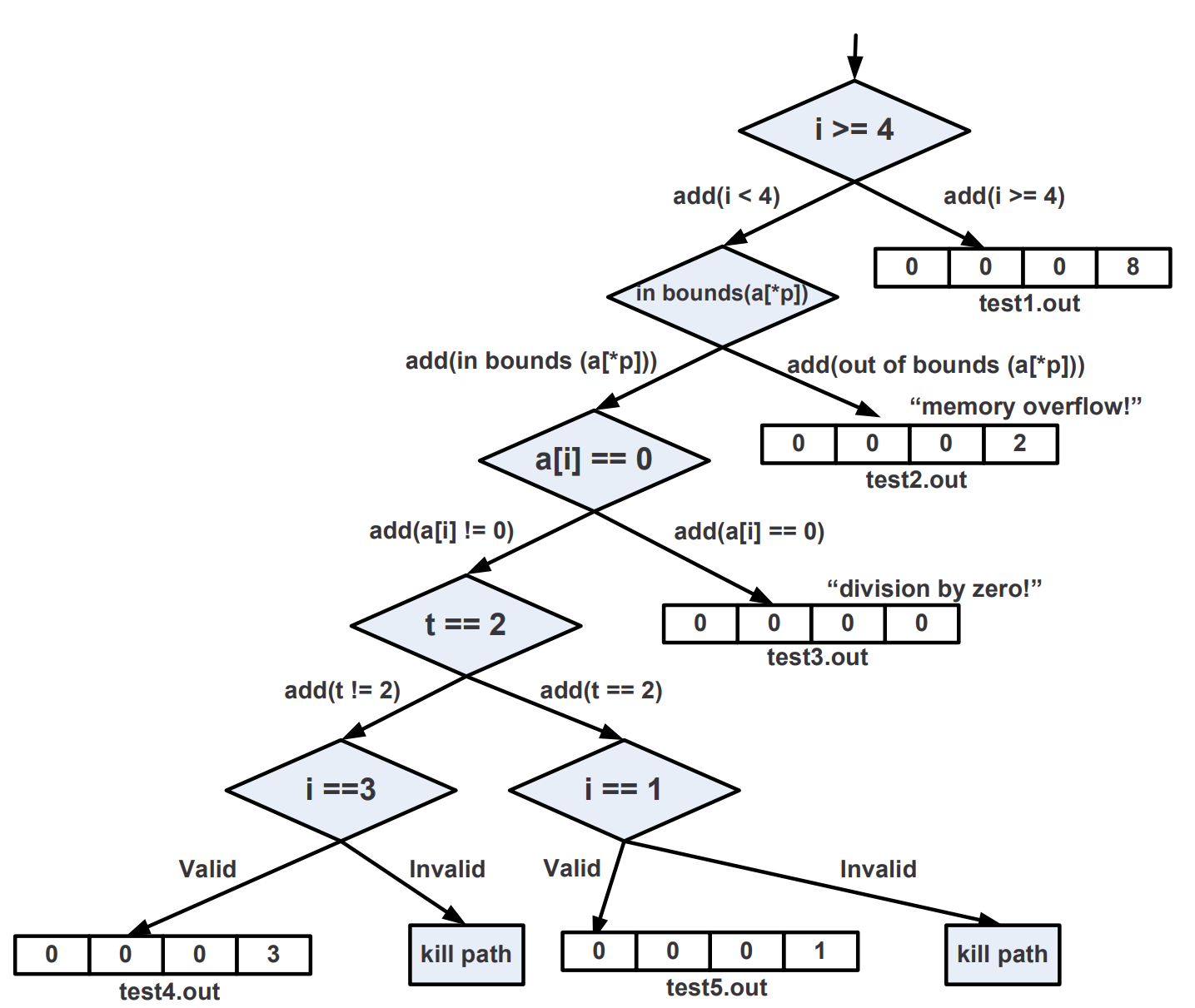
可以配合 EXE 论文中的配图理解

在上面的例子中，我们可以看到要实现符号执行，需要

收集执行路径上的约束条件
根据约束条件求解

后者比较（在现在相对比较）容易，有许多开源的优秀求解器可以实现，比如 z3。EXE 论文中自己实现了一个专为此类问题优化的求解器，这个我没仔细看，因为对实现求解器我不是很感兴趣。

那么如何实现收集执行路径的约束条件呢？我们不妨看看在符号执行里的比较有名的引擎，EXE 和 KLEE，二者的作者都是 EXE 论文的撰写者。KLEE 据说是在 EXE 工作上的重新实现。

EXE：EXE 提供了 exe-cc，这是一个从源码到源码的编译器。exe-cc 生成源码的细节论文中似乎并没有提到，生成的源码编译成可执行文件再进行符号执行。由于我也没有看过其实现，只能参照 KLEE 的实现，猜测他也是通过一个监视机来符号执行原来的 main 函数，并在条件判断处 fork 收集约束条件。
KLEE：KLEE 是一个执行 LLVM bitcode 的虚拟机，在这个虚拟机中，klee 可以监视所有的条件判断，在碰到条件判断的时候，fork 执行流，在每条执行流上都加上对应的约束条件。

符号执行往往需要实现被测程序准备使用的所有操作，所以实现二者这样的引擎需要相当可观的工作量。像 KLEE 这样的 LLVM bitcode 虚拟机，需要实现大部分的 LLVM IR。

工作量可观是一方面，另外以虚拟机的方式执行，也会降低性能。

Concolic Execution

在 2005 年发表的 DART 论文中，首次将符号执行（symbolic exectuion）和实际执行结合，后来这种技术被称为 concolic execution，即混合符号执行，concolic 这个词是 concrete 和 symbolic 的结合。

所谓的实际执行，就是 concrete execution 的翻译。concrete execution 是指，直接执行（被插桩的）被测代码（被测代码被直接以 native 的方法执行，不再像 KLEE 那样用一个虚拟机监视）。同时在执行的过程中，同步进行符号执行。不过要注意的是，这个同步的符号执行，仅仅只收集执行路径上的约束条件，也就是每次碰到分支的时候，都记录此时满足的约束条件，并不会调用求解器求解，这也是我们可能需要对被测目标插桩的缘故——需要在出现分支时记录约束条件。在一次执行完成后，我们就获得了一个约束集，代表特定执行路径在每个分支上应该满足的条件。我们记这个约束集为 $Constraints$，然后执行如下类 C++ 伪代码的操作

for (int i = 0; i < constraints.size(); i++) {
	new_constraints = constraints;
	new_constraints.resize(i);
	new_constraints.push_back(negate(constraints[i]));
	inputs.add(solver.solve(new_constraints));
}

在这段代码里，negate 函数是把约束取反，比如把 $x \leq 4$ 取反为 $x > 4$，当然实际上，只要添加这样的约束就可以了：$constraint == false$，比如 $(x \leq 4) = false$。solver.solve() 就是用于求解可以满足特定约束的解的求解器。

这样我们可以获得一些能够执行与当前执行流路径不同的输入，用这些输入再进行 concrete execution，就可以获得新的约束集，然后再求解新的输入，最后（对于没有随机性的程序在理论上）就可以实现 100% 的覆盖率。

Difference

在 KLEE 的 issue 中有这样一个提问 why on earth is concolic execution better?。其中我们就可以看到符号执行和混合符号执行的异同。

从搜索模式上来看，符号执行大多是广度优先搜索的，他们会在碰到分支的时候 fork 执行。而混合符号执行则是深度优先的，他会先完整执行完一条路径，然后再尝试别的路径。
- 这样来看，混合符号执行更有利于快速的获得能够触及被测程序极端情况（corner case）的输入，如果只是想寻找 bug，混合符号执行可能能够更快地触及他们
If you just want to find bugs, concolic execution might be better as you will reach deeper parts of the program quicker
- 但是符号执行不会重复执行已经执行过的程序部分，所以如果希望探索整个程序，符号执行会更为合适
If you want to fully explore all the paths classical symbolic execution will use less resources, because it won’t re-execute parts of the program unnecessarily
从执行方式上来看，混合符号执行在动态执行上是“native”的，相对在虚拟机上执行的符号执行，会更为轻量，速度也会更快。
- 不过对于 GitHub issue 上的解答 Notice that this is lightweight as you don't interfere with the running of the program much and use the solver to just get new inputs.，我个人觉得在符号执行也可以通过合适的优化来尽量少的调用求解器求解，这一点上可能影响会比较小。
从实现上来看，实现一个特定的可用混合符号执行的代价会较小
- 符号执行需要实现一个完整的虚拟机才能对一般的代码进行符号执行
- 混合符号执行是使用 concrete 的值进行执行的，那么对于我们没有实现的类型和操作，可以直接舍去值的 symbolic 部分，退化到纯粹的 concrete execution，这样只会丢失一些路径，但是还是可以探索一部分路径的

当然应该还有一些别的区别，比如资源的占用，路径爆炸问题的缓解等，我没仔细想，先不说了。

concolic execution of C in C++ —— A simple demo

这里的实现，我完全参考了 cs6.858 的对 python 的 concolic execution lab 的实现。这个 lab 属实很有意思，值得一写（代码量不大，又可以理解一个 concolic execution 的实现）。不过很遗憾，我并没有通过他的所有 check，却也不想对着我的散装 python 代码 debug，仔细一想，不然自己拿熟悉的语言实现一个类似的 concolic executor，所以就有了这个 concolic-cpp

这是一个可以混合符号执行一个 C 语言（极小子集）函数的符号执行引擎。虽然实际上按混合符号执行的特点，执行完整的 C++ 代码（并进行有限的混合符号执行）都是可以的，这里说是 C 语言，是因为我没有考虑过怎么支持复杂的 C++ 语法，说是 C 语言的极小子集，是因为目前我只实现了 int 类型（而且并没有加上类型范围的限制）和相关的 + == != 运算符。完成剩下的部分大体就是体力活了。对于别的 C 语言基本类型，我准备在未来尝试使用宏模板生成（我也考虑过使用 C++ 模板生成，但是感觉有些困难）。由于最近比较忙，所以这些工作可能会在未来我想起来的时候完善。

整个引擎主要分三部分

class Ast 和他的一些 subclass，它用来描述约束条件，是在实际使用的约束引擎（此引擎使用了 z3）上添加的一层抽象
- 之后会提为什么要添加这样一层，虽然在程序的当前情况下并没有特别体现
class Executor，此类用于混合符号执行目标函数
class Concolic*，这些类是对基本类型的 warpper

Concolic part

先来看 Conoclic 类的实现，以 ConcolicInt 为例，该类声明如下

class ConcolicInt {
 public:
  // for debug
  virtual std::ostream& dump(std::ostream& o) const;

  void set_concrete(int x);
  int concrete();

  ConcolicInt(const char* var_name);
  ConcolicInt(const char* var_name, const int init_val);
  ConcolicInt(const int init_val);
  ConcolicInt();
  virtual ~ConcolicInt() = default;

  ConcolicInt(AstPtr symbolic, int concrete);
  ConcolicInt(const ConcolicInt& concolic_int);
  ConcolicInt(ConcolicInt&& concolic_int) noexcept;

  ConcolicInt& operator=(const ConcolicInt& concolic_int) = default;
  ConcolicInt& operator=(ConcolicInt&& concolic_int)      = default;
  ConcolicInt& operator=(const int concrete_int) noexcept;

  ConcolicInt operator+(const ConcolicInt& rhs) const;
  ConcolicInt operator+(const int rhs_int) const;
  friend ConcolicInt operator+(const int lhs, const ConcolicInt& rhs);

  bool operator==(const ConcolicInt& rhs) const;
  bool operator==(const int rhs) const;
  friend bool operator==(const int lhs, const ConcolicInt& rhs);

  bool operator!=(const ConcolicInt& rhs) const;
  bool operator!=(const int rhs) const;
  friend bool operator!=(const int lhs, const ConcolicInt& rhs);
  operator int() const;

 private:
  AstPtr symbolic_;
  int concrete_;
};
ConcolicInt operator+(const int lhs, const ConcolicInt& rhs);
bool operator==(const int lhs, const ConcolicInt& rhs);
bool operator!=(const int lhs, const ConcolicInt& rhs);

std::ostream& operator<<(std::ostream& o, const ConcolicInt& c);

与 python 之类的语言不同，对于 C++ 我们并不能简单的把输入设置为 ConcolicInt 类，然后就一路把该类“传播“到被测函数里面（python 只要继承 int 类就可以了，再加之 python 是动态类型的，所以很容易）。如果不对源码动点手脚，传入的符号很快就会退化成 concrete value。想象这样的情况

int testf(int x) {
	...
}

可以传入 ConcolicInt，然后 x 会通过 ConcolicInt::operator int() 被赋值，整个测试都无法开展。

我的解决方法是添加一个头文件，直接把 int 用宏定义替换为 ConcolicInt

// concolic.h
#pragma once

#include "concolic-int.h"

#define int ConcolicInt

被测程序 include 这个头文件后，在编译时，所有的 int 就都会被替换成 ConcolicInt 了。然后需要提供基本类型应该支持的构造函数，也就是这两个

  ConcolicInt(const int init_val);
  ConcolicInt();

就可以提供对普通定义的支持了。其实现如下

ConcolicInt::ConcolicInt(const int init_val)
    : symbolic_(AstConstInt::make(init_val)), concrete_(init_val) {}
ConcolicInt::ConcolicInt() : symbolic_(AstConstInt::make(0)), concrete_(0) {}

AstConstInt 是我们表示一个常整数的 Ast 子类。对于无初始化的定义，直接默认初始化为 0。那么对于

#include "concolic.h"

...
int a;
int b{10};
...

这样的定义，a 会被初始化为 {symbolic: 0, concrete: 0}，b 会被初始化为 {symbolic: 10, concrete: 10}。还提供了这两个构造函数

ConcolicInt::ConcolicInt(const char* var_name)
    : symbolic_(AstInt::make(var_name)), concrete_(0) {}
ConcolicInt::ConcolicInt(const char* var_name, const int init_val)
    : symbolic_(AstInt::make(var_name)), concrete_(init_val) {}

这是为了生成 symbolic input 的，类似于 EXE 的 make_symbolic。在 Executor 类中我添加了一个简单的 warpper 函数，让我们可以方便的获得一个符号变量

[[nodiscard]] ConcolicInt& Executor::mk_int(const char* var_name) {
  std::string name{var_name};
  concolic_ints_.emplace(name, ConcolicInt{var_name});
  return concolic_ints_[name];
}

需要 warpper 是因为 Executor 类需要持有所有 symbolic input 的引用才能在未来调用求解器获得新的 input 的时候改变 input。

然后我们利用 C++ 的运算符重载，就可以实现插桩维护 symbolic value 的 symbolic 值和收集约束信息

暂时只重载了 + 号运算符，看看他的实现

ConcolicInt ConcolicInt::operator+(const ConcolicInt& rhs) const {
  ConcolicInt res{AstAdd::make(symbolic_, rhs.symbolic_),
                  concrete_ + rhs.concrete_};
  return res;
}

对于 concrete 部分直接相加即可，对于符号部分使用 Ast 子类的 AstAdd 生成。

还有 == 运算符，这个比较重要，为了简单起见，我们认为所有的逻辑运算都会造成分支（逻辑运算不一定会造成分支，但是分支一定有逻辑运算，过近似）。所以在这个运算符里面不仅要维护 symbolic 和 concrete value，还要添加约束

bool ConcolicInt::operator==(const ConcolicInt& rhs) const {
  auto b = ConcolicBool(AstEq::make(symbolic_, rhs.symbolic_),
                        concrete_ == rhs.concrete_);
  return b;
}

约束由这里的 ConcolicBool 来记录

ConcolicBool::ConcolicBool(AstPtr symbolic, bool concrete)
    : symbolic_(std::move(symbolic)), concrete_(concrete) {
  // NOTE: symbolic has been moved to symbolic_, use that instead
  Executor::get().addConstraint(
      AstEq::make(symbolic_, AstConstBool::make(concrete))->_z3expr());
}

他会向 executor 里添加约束。注意这里在添加不带符号变量的表达式（也就是可以化简成 true 和 false 的表达式），不应该添加到约束集里，我并没有在我的 demo 里做这个判断。

Ast part

上面一直没有提到 Ast 类是怎么实现的，其实思路是简单的，他们只要提供的统一的接口来返回约束器使用的表达式

class Ast {
 public:
  virtual std::ostream& dump(std::ostream& o) const;
  [[nodiscard]] virtual z3::expr _z3expr() const = 0;
  virtual ~Ast()                                 = default;

 private:
};

在 _z3expr 里每个 Ast node 都要返回对应的表达式，以二元操作 == 为例，他先继承 AstBinaryOp 类

class AstBinaryOp : public Ast {
 public:
  [[nodiscard]] z3::expr _z3expr() const override = 0;

  AstBinaryOp(AstPtr lhs, AstPtr rhs)
      : lhs_(std::move(lhs)), rhs_(std::move(rhs)) {}

 protected:
  AstPtr lhs_;
  AstPtr rhs_;
};

这个类存储了二元运算符的两个操作数，然后

class AstEq : public AstBinaryOp {
 public:
  [[nodiscard]] z3::expr _z3expr() const override;

  static AstPtr make(const AstPtr& a, const AstPtr& b) {
    return std::make_shared<AstEq>(a, b);
  }

  using AstBinaryOp::AstBinaryOp;

 protected:
};

z3::expr AstEq::_z3expr() const { return lhs_->_z3expr() == rhs_->_z3expr(); }

实现虚方法 _z3expr 即可。这样调用任意 Ast 的根节点，都能获得表示整棵树的表达式。

之前没有提到为什么要设计 Ast 类来自己描述约束的抽象语法树。主要的原因是 z3 这样的求解器虽然提供了 simplify 方法来化简表达式，但是它不能保证对于两个等价的式化简出同样的表达式，实际上这样的操作也不是 z3 这样的求解器所擅长的。如果想要很好的判断两个表达式相同，自己在 ast 上化简效果可能会更好。

判断两个表达式相同的需求是未来在对获取的约束集取反的时候剪枝时所引入的。这是 Executor 需要做的事。

Executor part

executor 的核心是这个 exec 函数

  template <typename FUNC, typename... ARGS>
  void exec(FUNC func, ARGS&... args) {
    current_iter_++;
    if (current_iter_ >= max_iter_) {
      return;
    }
    concolic_cpp_file_output("{\"input\": ", concolic_ints_, ",");
    auto ret = func(args...);
    concolic_cpp_file_output("\"returned\": ", ret,
                             ",\n\"explored\": ", constraints(), "},");
    for (const auto& explored_constraint : constraints()) {
      constraint_checked.insert(explored_constraint.to_string());
    }

    std::vector<z3::expr> old_constraints{constraints()};
    auto n_constraints = constraints().size();
    for (size_t i = 0; i < n_constraints; i++) {
      auto force_constraints           = forceBranch(old_constraints, i);
      const auto forced_constraint_str = force_constraints[i].to_string();
      if (constraint_checked.find(forced_constraint_str) !=
          constraint_checked.end()) {
        continue;
      } else {
        constraint_checked.insert(forced_constraint_str);
      }
      if (!findInputForConstraint(force_constraints)) {
        continue;
      }
      state.reset();
      exec(func, args...);
      if (current_iter_ >= max_iter_) {
        return;
      }
    }
  }

在这里的过程是

使用当前输入执行被测代码，收集约束集
遍历约束集，使用 forceBranch 来分别对每个约束取反
调用 findInputForConstraint 来求出对应约束集的 set 输入，递归调用 exec 传入新的 input。

从设计上我把 Executor 变成了单例，这是因为 z3 需要上下文来生成表达式，而我偷懒的使用了一个全局的 z3ctx 来生成所有的 z3 表达式，那么 Executor 也得是全局单例了。

use it！

使用这样的测试代码

#include "unistd.h"
#include "executor.h"
#include "concolic.h"

int testf(int a, int b) {
  for (; a != 10; a = a + 1) {
  }

  if (a == b) {
    return a + b;
  } else {
    if (a == 1) {
      return a + 4;
    } else {
      return b;
    }
  }
}

int32_t main() {
  auto& a = Executor::get().mk_int("a");
  auto& b = Executor::get().mk_int("b");

  Executor::get().exec(testf, a, b);
}

a，b 都会是符号遍历，初始化分别为 {symbolic: ‘a’, concrete: 0}，{symbolic: ‘b’, concrete: 0}，然后使用 exec 执行，编译执行 concolic-cpp-test 2>/dev/null，可以获得这样的输出：

{"input":  { "a":{"symbolic": "a", "concrete": 0},"b":{"symbolic": "b", "concrete": 0}} , 
"returned":  {"symbolic": "b", "concrete": 0} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(not (= a 3))","(not (= a 2))","(not (= a 1))","(= a 0)","(not (= a (+ (- 10) b)))","(not (= a (- 9)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 10},"b":{"symbolic": "b", "concrete": 0}} , 
"returned":  {"symbolic": "b", "concrete": 0} ,
"explored":  [ "(= a 10)","(not (= a b))","(not (= a 1))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 10},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a b)", "concrete": 20} ,
"explored":  [ "(= a 10)","(= a b)"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 9},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(= a 9)","(= a (+ (- 1) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 9},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(= a 9)","(not (= a (+ (- 1) b)))","(not (= a 0))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 8},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(= a 8)","(not (= a (+ (- 2) b)))","(not (= a (- 1)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 8},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(= a 8)","(= a (+ (- 2) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 7},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(= a 7)","(= a (+ (- 3) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 7},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(= a 7)","(not (= a (+ (- 3) b)))","(not (= a (- 2)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 6},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(= a 6)","(not (= a (+ (- 4) b)))","(not (= a (- 3)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 6},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(= a 6)","(= a (+ (- 4) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 5},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(= a 5)","(= a (+ (- 5) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 5},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(= a 5)","(not (= a (+ (- 5) b)))","(not (= a (- 4)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 4},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(= a 4)","(not (= a (+ (- 6) b)))","(not (= a (- 5)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 4},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(= a 4)","(= a (+ (- 6) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 3},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(= a 3)","(= a (+ (- 7) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 3},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(= a 3)","(not (= a (+ (- 7) b)))","(not (= a (- 6)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 2},"b":{"symbolic": "b", "concrete": 11}} , 
"returned":  {"symbolic": "b", "concrete": 11} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(not (= a 3))","(= a 2)","(not (= a (+ (- 8) b)))","(not (= a (- 7)))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 2},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(not (= a 3))","(= a 2)","(= a (+ (- 8) b))"] }, 
{"input":  { "a":{"symbolic": "a", "concrete": 0},"b":{"symbolic": "b", "concrete": 10}} , 
"returned":  {"symbolic": "(+ a 1 1 1 1 1 1 1 1 1 1 b)", "concrete": 20} ,
"explored":  [ "(not (= a 10))","(not (= a 9))","(not (= a 8))","(not (= a 7))","(not (= a 6))","(not (= a 5))","(not (= a 4))","(not (= a 3))","(not (= a 2))","(not (= a 1))","(= a 0)","(= a (+ (- 10) b))"] },

in the future

这样的作法（即使完成所有的 C 语言基本操作后）只能做到源代码级别的分析，我有兴趣在 LLVM IR 上做一个类似的引擎，以后有空了可以写一个玩玩。

More Works

符号执行本身作为一种软件测试方法，在 bug finding 上已有一定成果（EXE，KLEE 都有发现真实的漏洞）。不过也有把符号执行和模糊测试结合的测试方法，一般的思路是希望使用符号执行来为模糊测试提供高质量的语料。比如有 KLEE 和 AFL 结合的 kleefl。不过我个人感觉，对于 KLEE 这样的符号执行引擎，由于它在判断危险操作的时候，比如数组操作，已经会使用下标的所有取值来判断是否可能越界，如果 KLEE 没有报错，那基本就是 safe 的，模糊测试能够在语料上变异出什么能触发数组越界的输入的可能也十分有限。也就是说 KLEE 在进行测试时的（时间）代价和覆盖率以及正确性都已较高，模糊测试在这时更多能做的只是类似于（堆）内存的 double free 检测这样的工作。

而如果希望是模糊测试为主角，我认为使用混合符号执行来生成语料会更好：由混合符号执行来轻量快速地生成高质量语料，模糊测试变异器更多地进行非破坏性变异来进行探索。另外，直接在混合符号执行引擎上拓展出一个模糊测试器也是比较容易的，也可以比较容易的和 address sanitizer 这样的工具整合。对于这个我也有一定兴趣，未来有空也可以写一个玩玩。